El algoritmo conocido como Filtro de Kalman, utilizado en el guiado de las naves Apolo hacia la Luna, está permitiendo conocer y predecir la evolución de la pandemia del Coronavirus en distintas regiones y países. Es otra aplicación, desarrollada durante el Programa Apolo, que ayuda, más de sesenta años después, a la Humanidad.
PERO ¿QUÉ ES EL FILTRO DE KALMAN?
Un Filtro de Kalman permite estimar la evolución más probable (estadísticamente y de acuerdo con las incertidumbres inicialmente supuestas) del estado de un sistema dinámico (es decir, que evoluciona con el tiempo), y puede ser generalizado al caso no lineal, así como incorporar la estimación de los propios parámetros del modelo. Dicho de un modo más mundano; es una fórmula, una función, un método estadístico, que permite predecir el futuro en base a unas condiciones iniciales.
¿QUIÉN LO DESARROLLÓ Y CUÁNDO LO HIZO?
El Filtro de Kalman debe su nombre a Rudolf E. Kalman, un ingeniero húngaro nacido en 1930 cuya familia emigró a Estados Unidos en plena Segunda Guerra Mundial. En 1953 obtuvo el título de Ingeniero eléctrico por el MIT. Siete años después, en 1960, Kalman publicó su famoso artículo en donde desarrollaba un conjunto de ecuaciones matemáticas que permitían (permiten) calcular y conocer el estado de un proceso. Lo tituló en inglés: “A new approach to linear filtering and prediction problems”.
¿QUÉ RELACIÓN TIENE EL FILTRO DE KALMAN Y EL PROGRAMA APOLO?
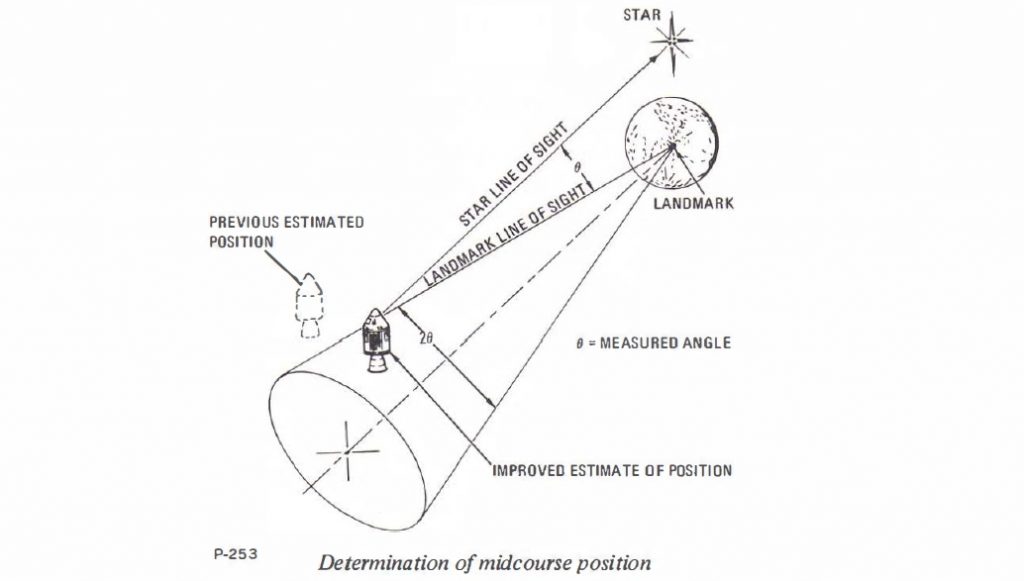
A principios de la década de los años 60, en pleno desarrollo del Programa Mercury y de la carrera espacial, la NASA había heredado la experiencia de NACA en el control de vuelo y tenía a ingenieros ya trabajando en el problema del guiado de naves espaciales. El responsable de este grupo de investigadores era Stanley Schmidt, del Centro de Investigación Ames en Palo Alto, que apoyaba al Space Task Group con sus estudios sobre navegación lunar.
En el otoño de 1960, el Doctor Kalman organizó una reunión con Schmidt y fue allí, en ese afortunado encuentro, donde Kalman presentó su famoso trabajo. A partir de ahí se comprobó que el trabajo de Kalman podía proporcionar una solución al problema de la navegación espacial a la Luna haciendo alguna modificación a la formulación original puesto que el método original de Kalman requería que los astronautas estuvieran tomando medidas continuamente, algo muy poco práctico en la realidad. Esas nuevas ecuaciones son conocidas como el Filtro de Kalman Extendido (EKF en sus siglas en inglés). Aunque para ser precisos, el último empujón lo realizó el propio Schmidt obteniendo la solución “no lineal” con el llamado Filtro Schmidt-Kalman.
En cualquier caso, el modelo matemático inventado por Kalman y actualizado por Schmidt, sigue siendo considerado, hoy en día, como una de las herramientas tecnológicas fundamentales que permitieron al hombre pisar la Luna bajo el Programa Apolo.
EL FILTRO DE KALMAN Y EL COVID-19
Lo bueno del Filtro de Kalman es que puede ser usado en multitud de campos, no solo en el de la navegación espacial. Uno de esos campos es el de la medicina. En concreto se puede utilizar para el estudio de la evolución de una epidemia, como la producida por el virus SARS-CoV-2.
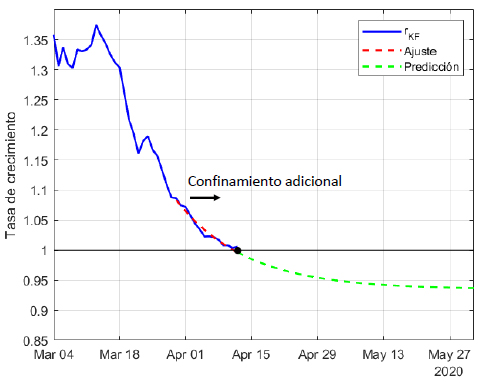
En España se han realizado estudios en este sentido, con el fin de ayudar en el control y seguimiento de la pandemia. Un ejemplo es el trabajo realizado por Antonio Gómez Expósito, José A. Rosendo Macías y Miguel A. González Cagigal, de la Universidad de Sevilla, en el que se determina el momento en el que se alcanzaría el pico de la pandemia. Por lo que se, en otros países también se ha utilizado el Filtro de Kalman con el mismo fin. Es el caso de Israel y el estudio de Ran Kremer de la Universidad de Bar-Ilan.
CONCLUSIÓN
Para aquellos que siguen afirmando que el Programa Apolo y la carrera espacial no mereció la pena, aquí tenemos una prueba más de que el desarrollo tecnológico realizado hace más de cincuenta años para conseguir llegar a la Luna, permite que hoy tengamos herramientas y aplicaciones para luchar contra la peor pandemia que ha sufrido la Humanidad en décadas.
ANOTACIONES RELACIONADAS:
- El nuevo MrGorsky y el Coronavirus.
- Conspiranoico, por Pantomima Full.
- 50 años del Apolo 11: un gigantesco salto para la humanidad.
